07. Risk Analysis

Risk and Uncertainty

We make decisions every day. However, possible outcomes of these decisions are not always clear. We say we are making decisions in situations under risk or uncertainty.

• Risk – an actual outcome is unknown but we can assign probabilities to each possible scenario.
  • Expected value, Expected utility theory
  • Prospect theory [Reference point]
• Uncertainty – we can not assign probabilities to each outcome.
  • Game theory [e.g. Prisoner’s dilemma]
    

Risk

• Credit:
  • Customer has been given credit and may default. This could be an actual loan or credit card account or credit in terms of time to pay.
• Investments.
• Fraud: insurance, warranty, deception.
• System failure: partial or total.
• Hostile attack causing damage.

Note

Risk is a measurable uncertainty.
Uncertainty is an unmeasurable risk.

A hazard is something that has the potential to harm you. risk is the likelihood of a hazard causing harm.

Risk management

In most commercial situations it is desirable to minimise risk by:

• ‘Wise’ choices between alternative customers, investments, systems - diversification.
• Financial precautions, like loan insurance – [moral hazard]
• Technical precautions: system protection or backup.
• Investigation to detect potential fraud or attacks.

Risk measure

• The return on investment can be represented by a probability distribution.
• This distribution is derived from historical data, tempered by contemporary opinions of ‘experts’ with domain knowledge.
• The expected value, or mean, of the distribution is an obvious measure of profitability and lack of risk.
• But the expected value tells us nothing about the spread of the consequences. For example, distribution may be bimodal, with a decent mean but high probability of significant loss.

Volatility

• Volatility is a measure of the dispersion of returns for a given security.
• The higher the volatility, the riskier the security.
• Typically, volatility are measured by using the standard deviation or variance between returns from that security.

Worst outcomes

• Decision makers are often interested in the probabilities of the worst things happening. (1% chance of getting nothing)
• Information in the tails of the distribution is lost when we consider the expected value.

Value at Risk (VaR)

• Timeframe
• Confidence level
• Loss amount

The Value at Risk corresponding to 𝛼 is the largest value of 𝑥 for which the probability of a loss of at least 𝑥 is (at least) 𝛼.

Alt text

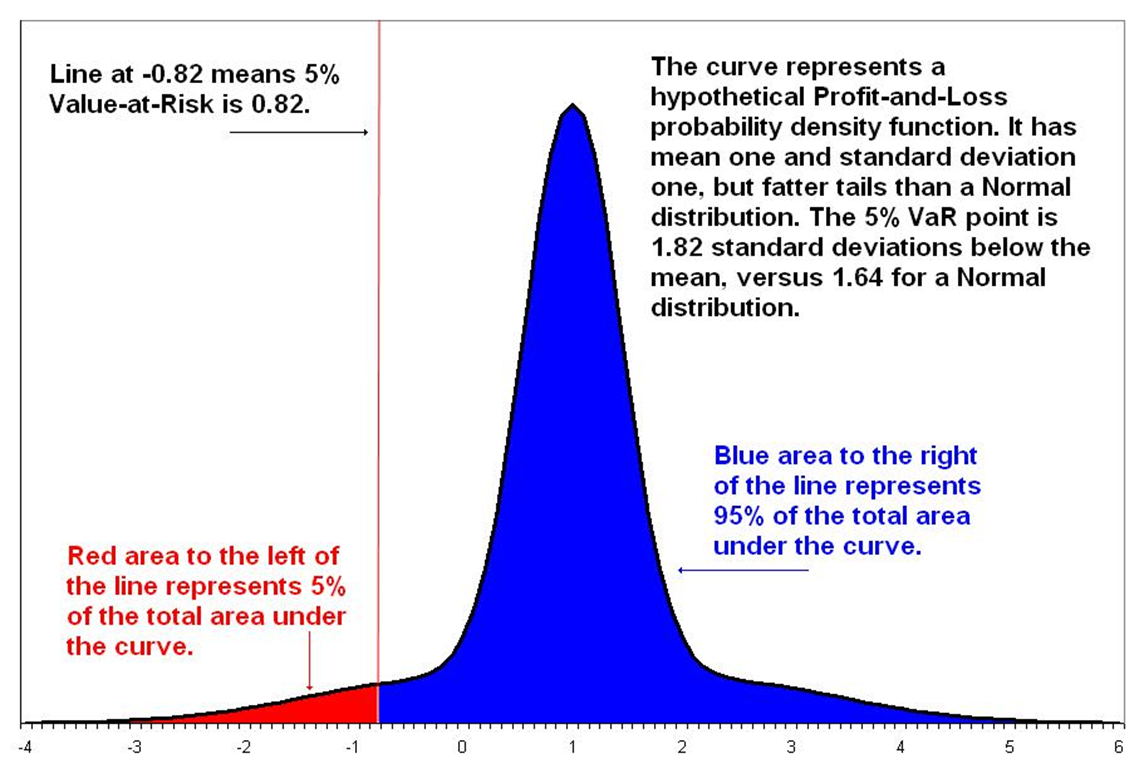
VaR Estimation

• Historical method – analyse historical data and find possible loss over the given time period
• Variance method – fit a distribution of profits/losses, e.g. $N(\mu ,{\sigma }^2)$, then find possible loss
• Monte Carlo (or bootstrapping) method – build a model, run it to generate synthetic historical data and use statistical analysis to determine worth case loss.

Problems with VaR

• Value at Risk can be misleading: false sense of security.
• VaR does not measure worst case loss – it says there is 1% probability that loss will be greater than VaR value but it does not say how big that loss can be.
• Value at Risk gets difficult to calculate with large portfolios
• Value at Risk is not additive. VaR for two assets does not equal the sum of individual VaRs.
• The resulting VaR is only as good as the inputs and assumptions.
• Different Value at Risk methods lead to different results.

Expected Tail Loss (ETL)

• ETL has many other names, including Expected Shortfall, Conditional Value at Risk (CVaR) and Average Value at Risk.
• Uses a threshold probability 𝛼. Given that the probability of loss is less than 𝛼, what is the expected loss?
• OR, given that the loss is at least $Va{R}_{\alpha }$, what is the expected loss?
  $ET{L}_{\alpha }=\frac{1}{\alpha }{\displaystyle {\int }_0^{\alpha }Va{R}_{\beta }d\beta }$
• Use a sum for a discrete distributions

Problems with VaR and ETL

• It can be very difficult (some say impossible) to estimate the probability of an extremely rare event.
• ‘Possible’ rare events may have never happened in the past.
• Unanticipated rare events will not be accounted for.

LTCM hedge fund

• Long Term Capital Management (LTCM) hedge fund was formed in 1993 and was founded by renowned Salomon Brothers bond trader John Meriwether along with Nobel-prize winning Myron Scholes of the Black-Scholes model and Robert Merton
• Started with more than $1 billion of capital
• Arbitrage strategy with risk level close to zero
• By 1998, LTCM had approximately $5 billion in assets, controlled over $100 billion and had trading positions worth over $1 trillion

Can risk be measured?

• Risk:

  • In some applications, there is a lot of data available and the extent of risk is limited, e.g. loans, credit cards etc.
  • Each customer can be assessed (e.g. credit scoring).

• Uncertainty:

  • Don’t try to predict a Black Swan event
  • Be prepared to a Black Swan event and its consequences

Reference

Tim's slides of Week 5