06.Data Stream(W7&8&9)

HaiyueOctober 19, 2023About 4 min

What's data stream

A data stream is a real-time, continuous, ordered (implicitly by arrival time or explicitly by timestamp) sequence of items. It is impossible to control the order in which items arrive, nor is it feasible to locally store a stream in its entirety.

Massive volumes of data, records arrive at a high rate

Applications of data stream processing

Stock monitoring (data analysis)

Stream of price and sales volume of stocks over time
Technical analysis/charting for stock investors
Support trading decisions

What kinds of work it could do

Usuage Examples

Notify me when the price of IBM is above $83, and the first MSFT price afterwards is below $27.
Notify me when some stock goes up by at least 5% from one transaction to the next.
Notify me when the price of any stock increases monotonically for ≥30 min.
Notify me whenever there is double top formation in the price chart of any stock
Notify me when the difference between the current price of a stock and its 10 day moving average is greater than some threshold value

Challenges of data stream processing

Case 1: Computation of daily electric power consumption by customer market segment from customer meter data

Join between several streams
Join between stream data and customer database

Solution: incremental computation and definition of temporal windows for joins

Case 2: 100 most frequent @S IP adresses on a router

Maintain a table of IP addresses with frequencies ?
Sampling the stream ?

Face high (and varying) rate of arrivals
Exact versus approximate answers

Windowing

Definition of windows of interest on streams

Fixed windows: September 2007
Sliding windows: last 3 hours
Landmark windows: from September $1^{st}$ , 2007

Window specification

Physical time: last 3 hours
Logical time: last 1000 items

Refreshing rate

Rate of producing results (every item, every 10 items, every minute, …)

Reservoir sampling

Problem: maintaining a random sample from a stream

Random sample of size M
- Fill the reservoir with the first M elements of the stream
- For element n (n > M)
  - Select element n with probability M/n
  - If element n is selected pick up randomly an element in the reservoir and replace it by element n

Random sampling from a sliding window

import random as rd
class ReservoirSample:
  def __init__(self, sample_size):
    self.__index__ = 0
    self.__sample_size__ = sample_size
    self.__sample_pool__ = []

  # Whether select the item n
  def __is_select__(self):
    return (rd.randint(1, self.__index__) <= self.__sample_size__)

  def pipe(self, data):
    self.__index__ += 1
    if(self.__index__ <= self.__sample_size__):
      self.__sample_pool__.append(data)
    else:
      if self.__is_select__():
        idx = rd.randint(0, self.__sample_size__ - 1)
        self.__sample_pool__[rd.randint(0, self.__sample_size__ - 1)] = data
  def get_samples(self):
    return list(self.__sample_pool__)

## Test code below
reservoir_obj = ReservoirSample(10)
for i in range(1000000):
  reservoir_obj.pipe(i)

## Get the final sample result
reservoir_obj.get_samples()

Implementation on google colab

Bloom filter

Problem: Given a large set S, check whether a new element i is in the set

Check if an IP address is in the black list
Check a login if this is an existing account

Algorithm:

Input: S has m elements from a data stream, memory size n, m>n
Output:

Returns TRUE -> there is a high chance that the element is in S
Returns FALSE -> when the element is not in S

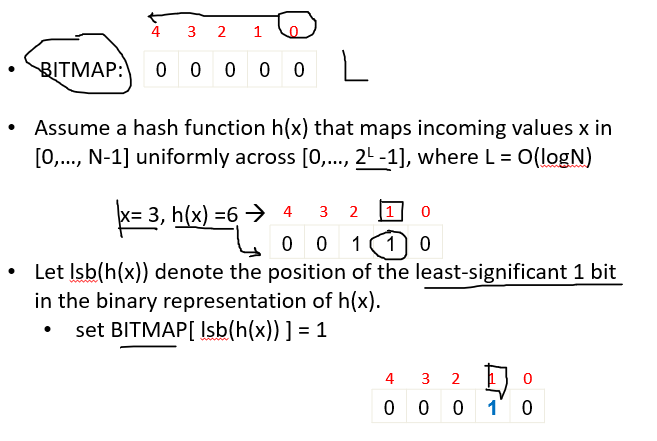
Consider a set of hash functions { $h_1,h_2,...,h_k$ }, $h_i:S\rightarrow [1, n]$
Step 1: Initialization
Set all n bits in the memory to 0.
Step 2: Insert new element a
Compute $h_1(a), h_2(a), ..., h_k(a)$ , Set the corresponding bits to 1.
Step 3: Check whether an element a is in $S$
Compute $h_1(a), h_2(a), ..., h_k(a)$ . If all the bits are 1, return TRUE, else, return FALSE.

Characters:

Given a large set of element S, efficiently check whether a new element is in the set.
Bloom filters use hash functions to check membership
- Return TRUE if there is high probability of the element is in S
- Return FALSE if the element is not in S
- False positive error rate depends on the size of S and the size of the memory

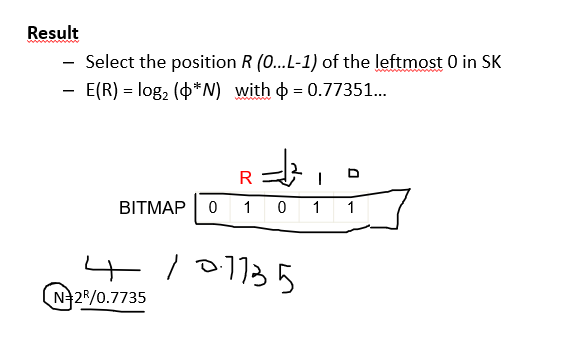
Hash (FM) sketch

Problem: Find the number of distinc values in a stream of values with domain [0,…N-1]

Distinct IP addresses in a router (networking monitoring)
Number of species in a population
Sampling and windowing may not work well

A $\leftarrow$ the best attribute for splitting the
Decision attribute for this node $\leftarrow$ A
For each value of A, create new child node
Split training {examples} to child nodes
if examples perfectly classified: Stop
else: iterate over new child nodes
Split(child_node, {subset of examples})

Ross Quinlan (ID3: 1986), (C4.5: 1993)
Breimanetal (CaRT: 1984) from statistics

A criterion for attribute selection

Which is the best attribute?
1. The one which will result in the smallest tree
2. Heuristic: choose the attribute that produces the “purest” nodes
Popular impurity criterion: information gain
1. Information gain increases with the average purity of the subsets that an attribute produces
Strategy: choose attribute that results in greatest information gain

The performance of split:

Infomation Gain
Entropy

The final decision tree

Note: not all leaves need to be pure; sometimes identical instances have different classes

Splitting stops when data can’t be split any further

Decision tree using data stream

Non-additive methods: the example of decision trees

VFDT: Very Fast Decision Trees (Domingos & Hulten 2000)

$X_1, X_2, …, X_p$ : discrete or continuous attributes
Y: discrete attribute to predict
Elements of the stream $(x_1, x_2, …, x_p, y)$ are examples
G(X): measure to maximize to choose splits (ex. Gini, entropy, …)

Hoeffding trees: not necessary to wait for all examples to choose a split

Maintain $G(X_j)$
Wait for a minimum number of examples, $n$
$X_j, X_k$ : the 2 variables with highest values of $G$
Split on $X_j$ when $G(X_j) - G(X_k) ≥ \varepsilon, \varepsilon = \sqrt{\frac{R^2ln(1/\sigma)}{2n}}$
Recursively apply the rule by pushing new examples in leaves of the tree

Clustering

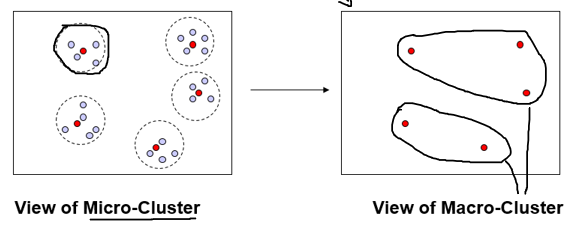
Clustream

Numerical variables
2 phases:
- Online phase: maintenance of a large number of 'micro-clusters' described by statistics of their contents
- Offline phase: use of micro-clusters to produce a final clustering.
Mechanism to keep track of micro-clusters history

Representation of micro-clusters

CVF: Cluster Feature Vector (BIRCH)
(n, CF1(T), CF2(T), CF1(X1), CF2(X2), …, CF1(Xp), CF2(Xp))
n: number of data points
CF1(T): sum of the time stamps $T_{i1}…T_{in}$
CF2(T): sum of the squares of the time stamps
$CF1(X_j) = \displaystyle\sum_{i=1..n}x_{ji}$
$CF2(X_j) = \displaystyle\sum_{i=1..n}x_{ji}^2$
Supports union/difference by addition/substraction
Incremental computation (elements are disgarded)

References

Week 7 Slides from Thuc (SP52023)
Week 8 Slides from Thuc (SP52023)
Week 9 Slides from Thuc (SP52023)