02.Bayesian networks(W3)

Bayesian networks: examples, definition

Details

Bayesian network 1

Bayesian Network 1

Bayesian network 2

Bayesian Network 2

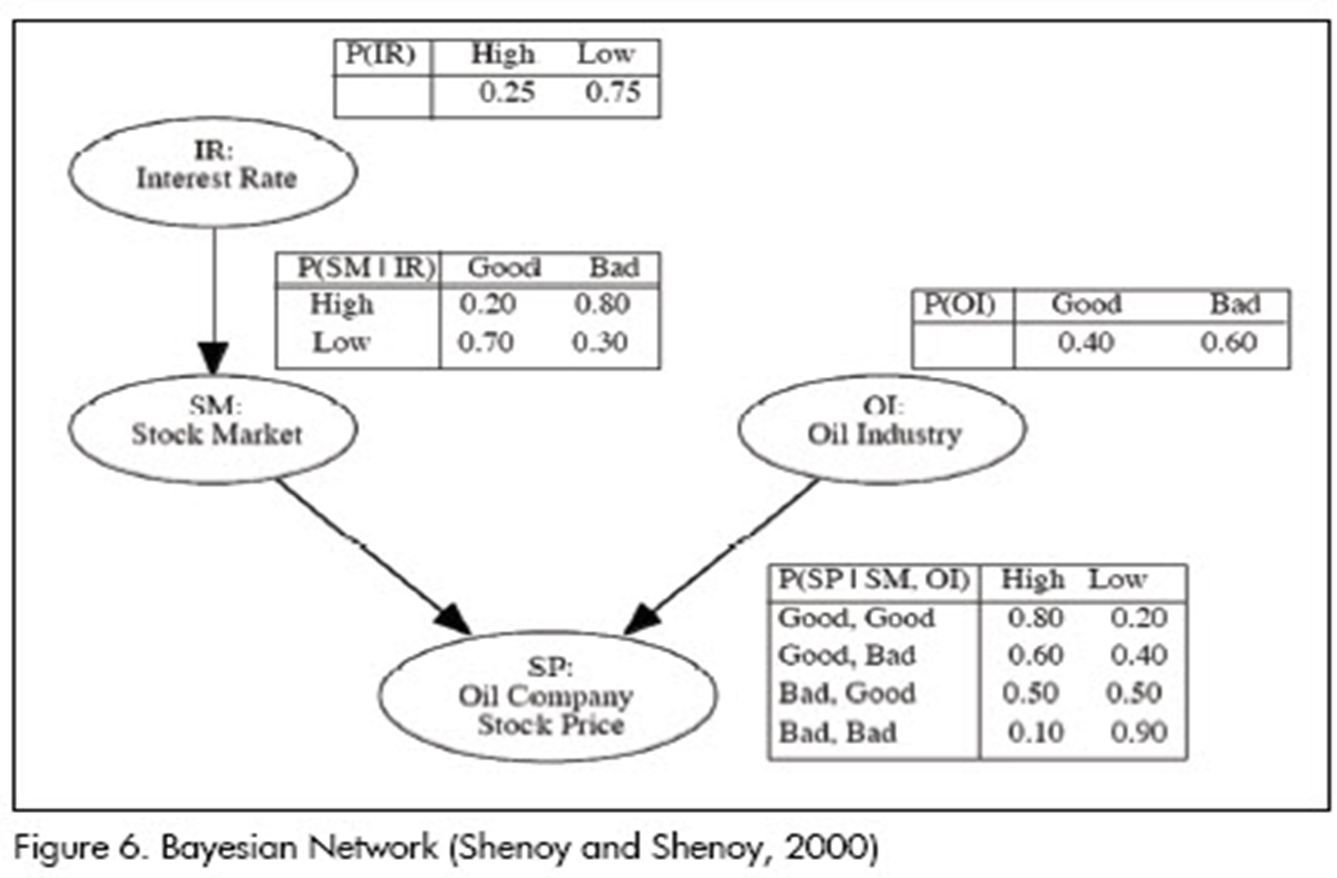
Bayesian networks

What is a BN?

A Bayesian network (BN) is a graphical model for depicting probabilistic relationships among a set of variables.

• BN Encodes the conditional independence relationships between the variables in the graph structure.
• Provides a compact representation of the joint probability distribution over the variables
• A problem domain is modeled by a list of variables $X_1, …, X_n$
• Knowledge about the problem domain is represented by a joint probability $P(X_1, …, X_n)$
• Directed links represent causal direct influences
• Each node has a conditional probability table quantifying the effects from the parents.
• No directed cycles

Two important properties of Bayesian Networks

1. Encodes the conditional independence relationships between the variables in the graph structure
2. Is a compact representation of the joint probability distribution over the variables

What is Markov blanket

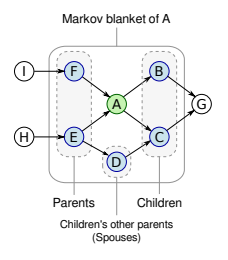
The set of nodes that graphically isolates a target node from the rest of the DAG is called its Markov blanket and includes:

• its parents;
• its children;
• other nodes sharing a child.
  Since $⫫_G$ implies $⫫_P$, we can restrict ourselves to the Markov blanket to perform any kind of inference on the target node, and disregard the rest.

References

1. Understanding Bayesian Networks - with Examples in R

Components of A Bayesian Network

A Bayesian Network is consisted with two components

1. A directecd Acyclic Graph

   Characteristics

   1. Each node in the graph is a random variable
   2. A node X is a parent of another node Y if there is an arrow from node X to node Y
      eg. A is a parent of B
   3. Informally, an arrow from node X to node Y means X has a direct influence on Y
2. A set of tables for each node in the graph
   

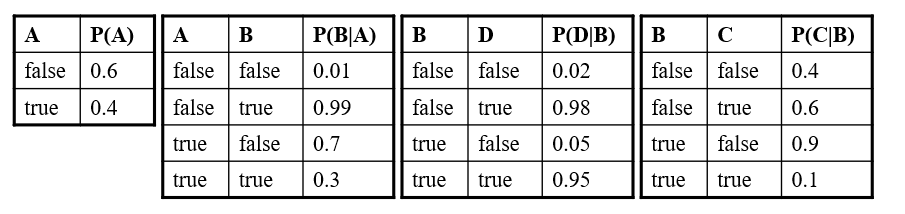
   Characteristics

   1. Each node $X_i$ has a conditional probability distribution $P(X_i | Parents(X_i))$ that quantifies the effect of the parents on the node
   2. The parameters are the probabilities in these conditional probability tables (CPTs)

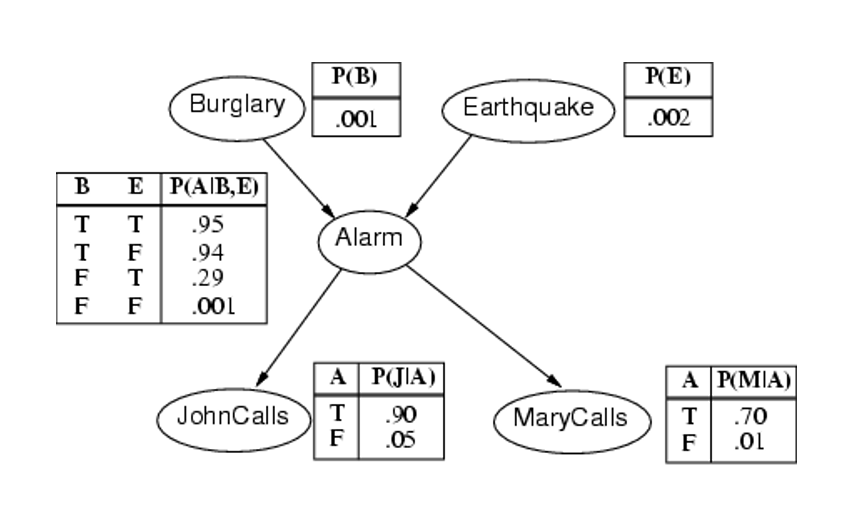
Bayesian Network Example

Using the network in the example, suppose you want to calculate:

$$\begin{equation} \begin{split} P(A = true, B = true, C &= true, D = true) \\ &= P(A = true) *\\ &\text{\ \ \ \ \ } P(B = true | A = true) *\\ &\text{\ \ \ \ \ } P(C = true | B = true) *\\ &\text{\ \ \ \ \ } P( D = true | B = true) \\ & = (0.4)*(0.3)*(0.1)*(0.95) \end{split} \end{equation}$$

Details for data refer to here.

Conditional Independence

The Markov condition: Given its parents (P1, P2), a node (X) is conditionally independent of its non-descendants (ND1, ND2).

The Joint Probability Distribution

Due to the Markov condition, we can compute the joint probability distribution over all the variables $X_1, …, X_n$ in the Bayesian net using the formula:

$P(X_1 = x_1, ..., X_n=x_n) = \prod_{i=1}^{n}P(X_i=x_i|Parents(X_i))$

Info

Where $Parents(X_i)$ means the values of the Parents of the node $X_i$ with respect to the graph

Bayesian network inference

• Using a Bayesian network to compute probabilities is called inference

• In general, inference involves queries of the form: $P( X | E )$

  E: The evidence variable(s)
  X: The query variable(s)

• Diagnostic (evidential, abductive): from effect to cause

  • P(Buglary|JonhCalls), P(B|J)=0.016
  • P(B|J,M)=0.29
  • P(A|J,M)=0.76

• Causal (predictive): From cause to effect

  • P(J|B)=0.86
  • P(M|B)=0.67

• Intercausal (explaining away): common effect

  • P(B|A)=0.38
  • P(B|A, E)=0.003

• Mixed: two or more of the above combined

  • P(A|J,E’)=0.03
  • P(B|J,E’)=0.017

• In general, the problem of Bayesian network inference is NP-hard (exponential in the size of the graph)

• Exact inference

  • Probability and Markov condition
  • Variable elimination
  • Clustering / join tree algorithms

• Approximate inference

  • Stochastic simulation / sampling methods
  • Markov chain Monte Carlo methods
  • Genetic algorithms
  • Neural networks
  • Simulated annealing
  • Mean field theory

• $P(X|E) = \frac{P(E|X)P(X)}{P(E)} = \frac{P(E,X)}{P(E)}$

• Marginalisation: $P(x) = \sum_yP(x,y)$
  e.g. $P(X,E) = P(X,E,A) + P(X,E,A')$, A is binary

• Markov condition: $I(X, NDx|Parent(X))$

• Diagnostic (evidential, abductive): from effect to cause
  

$$\begin{equation} \begin{split} P(B|J) &= \frac{P(B,J)}{P(J)}\\ \\ P(B,J) &= P(B,J,A) + P(B,J,A')\\ &= P(J|A,B)P(A,B) + P(J|A',B)P(A'B)\\ &= P(J|A)P(A,B) + P(J|A')P(A',B)\\ &= 0.9P(A,B) + 0.05P(A',B) \end{split} \end{equation}$$

$$\begin{equation} \begin{split} P(A,B) &= P(A,B,E) + P(A,B,E')\\ &= P(A|B,E)P(B,E) + P(A|B,E')P(B,E')\\ &= P(A|B,E)P(B)P(E) + P(A|B,E')P(B)P(E')\\ &= 0.95*0.001*0.002 + 0.95*0.001*0.998 \end{split} \end{equation}$$

---

$$\begin{equation} \begin{split} P(B|J=T) &= \frac{P(B,J)}{P(J)}\\ \\ P(J) &= P(J,A) + P(J,A')\\ &= P(J|A)P(A') + P(J|A')P(A')\\ &= P(A|B,E)P(B)P(E) + P(A|B,E')P(B)P(E')\\ &= 0.9P(A) + 0.05P(A')\\ \\ P(A) &= P(A,B,E) + P(A,B,E') + P(A, B',E) + P(A,B',E') \\ &= P(A| B,E)P(B,E) + ...\\ &=0.0025 \end{split} \end{equation}$$

$P(J) = 0.05212$
$P(B|J) = \frac{P(B,J)}{P(J)}$ = 0.016

$P(J|B) = \frac{P(B,J)}{P(B)}$
$P(B,J) = P(B,J,A) + P(B,J,A') = 0.00086$
$P(B) = 0.001$
$P(J|B) = \frac{0.00086}{0.001} = 0.86$

• Intercausal (explaining away): common effect
  $P(B|A) = \frac{P(A,B)}{P(A)}$
  $P(B,A) = 0.00095$
  $P(A) = 0.0025$
  $P(B|A) = \frac{0.00095}{0.0025} = 0.38$

Summary

• Bayesian networks

  • Definition
  • Properties: Markov condition, compact joint probability

• Bayesian networks inference

  • Understand how to use probability theory and Markov condition to do the inference for different types of queries
  • In practice, we are going to use R (gRain package)

• Next week, learning Bayesian networks from data

References

1. Naive Bayes Classifier
   Resource from Youtube
2. Week 3 Slides from Thuc (SP52023)