Information came from Srecko in Discord channel HS.resources at 1:50pm 07 July 2024.
CausalPrism: A Visual Analytics Approach for Subgroup-based Causal Heterogeneity Exploration
Abstract
In causal inference, estimating Heterogeneous Treatment Effects (HTEs) from observational data is critical for understanding how different subgroups respond to treatments, with broad applications such as precision medicine and targeted advertising. However, existing work on HTE, subgroup discovery, and causal visualization is insufficient to address two challenges: first, the sheer number of potential subgroups and the necessity to balance multiple objectives (e.g.., high effects and low variances) pose a considerable analytical challenge. Second, effective subgroup analysis has to follow the analysis goal specified by users and provide causal results with verification. To this end, we propose a visual analytics approach for subgroup-based causal heterogeneity exploration. Specifically, we first formulate causal subgroup discovery as a constrained multi-objective optimization problem and adopt a heuristic genetic algorithm to learn the Pareto front of optimal subgroups described by interpretable rules. Combining with this model, we develop a prototype system, CausalPrism, that incorporates tabular visualization, multi-attribute rankings, and uncertainty plots to support users in interactively exploring and sorting subgroups and explaining treatment effects. Quantitative experiments validate that the proposed model can efficiently mine causal subgroups that outperform state-of-the-art HTE and subgroup discovery methods, and case studies and expert interviews demonstrate the effectiveness and usability of the system. Code is available at OSF.
Key Information
Two challenges for causal visualization:
- The sheer number of potential subgroups and the necessity to balance multiple objectives (e.g.., high effects and low variances) pose a considerable analytical challenge.
- Effective subgroup analysis has to follow the analysis goal specified by users and provide causal results with verification.
Solution:
propose a visual analytics approach for subgroup-based causal heterogeneity exploration
How to do:
- formulate causal subgroup discovery as a constrained multi-objective optimization problem
- adopt a heuristic genetic algorithm to learn the Pareto front of optimal subgroups described by interpretable rules
Output: a prototype system, CausalPrism
Characters of the system
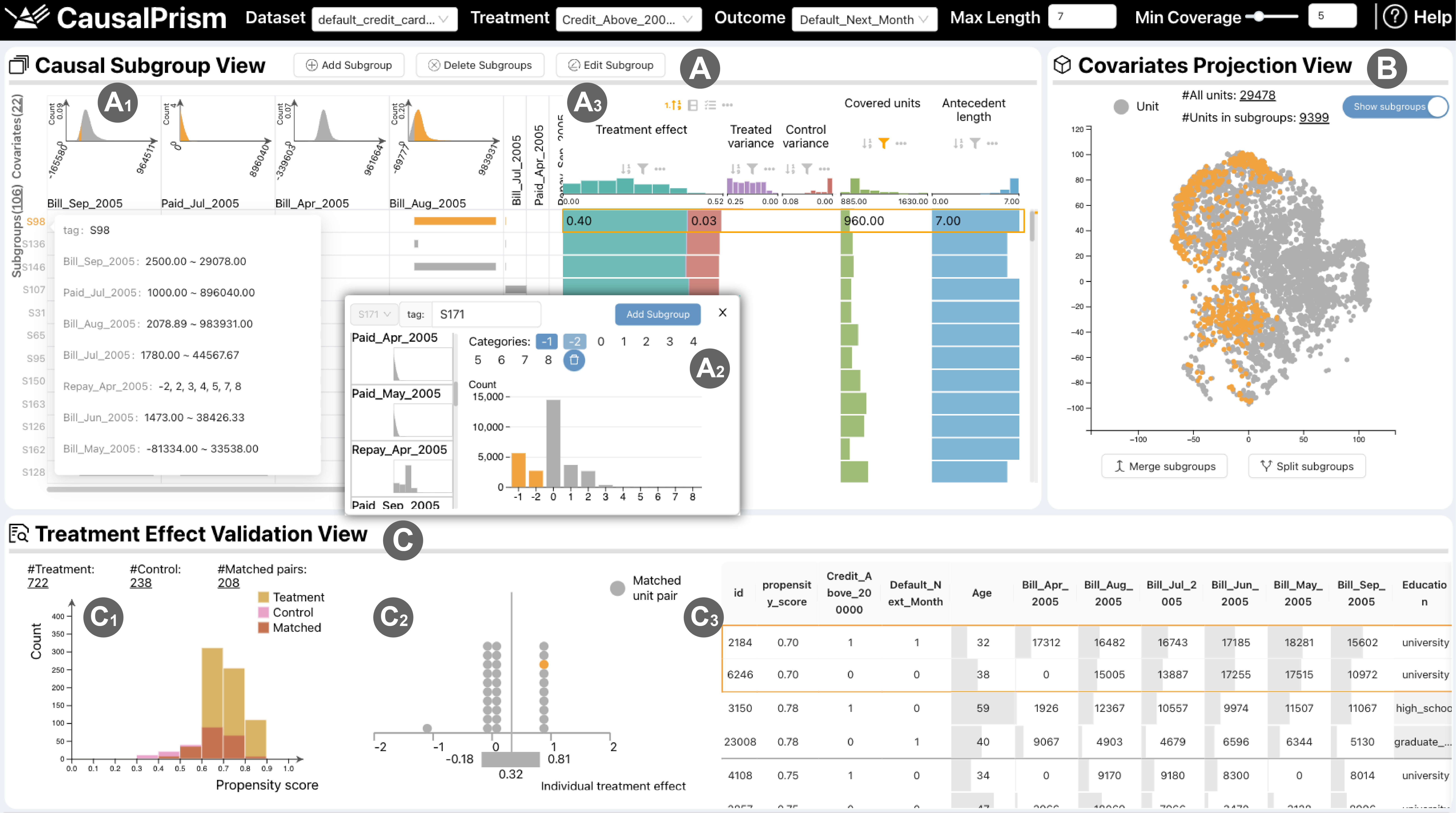
Incorporates tabular visualization, multi-attribute rankings, and uncertainty plots to support users in interactively exploring and sorting subgroups and explaining treatment effects
Introduction
Causal inference is a data analysis process aiming at conclusions about whether and to what extent treatments affect outcomes [48]. Data heterogeneity must be considered when estimating treatment effects, as the effect of the same treatment may vary across subgroups. As shown in Fig. 1, subgroups within the population responded differently to the treatment. The treatment exerts larger effects on Subgroup 1 and Subgroup 3 than Subgroup 2. Nevertheless, the high variance of Subgroup 1 indicates that individual differences (uncertainty of the outcome) exist. Discovering those subgroups with strong treatment effect and low outcome variance (hereinafter referred to as significant treatment effect) compared to the overall population is widely used in domains such as healthcare [50], marketing [56], and public administration [23]. For example, marketers want to find customer groups where advertising more effectively drives purchases. Since Randomized Controlled Trials (RCTs), known as the gold standard for causal inference [31], are not always feasible due to cost or ethical concerns, there is a strong need to uncover those causal subgroups from observational data effectively.
Key Information
The function of Causal inference: aims at conclusions about whether and to what extent treatments affect outcomes
In practical applications, analyzing causal heterogeneity faces two challenges. First, it is nontrivial and challenging to identify important subgroups from a large number of subgroup candidates. Subgroups can be described by different combinations of variables, which could lead to a combinatorial explosion of candidates. Selecting optimal subgroups requires trade-offs among various targets in the objective space, such as effect strength, outcome variance, and subgroup coverage, further complicating the subgroup discovery process. Coordinating the above factors has to follow users’ analysis requirements. Nevertheless, the identification model can hardly communicate with humans due to the lack of interpretability, which causes the second challenge. The subgroups obtained by the black-box model may hardly be interpreted by or fail to support analysis tasks. Users still need to tediously analyze and compare multiple subgroups to determine which one they prefer. In addition, without a treatment effect explanation, numerical causal conclusions alone are difficult to convince users, especially in high-stakes safety and life-critical fields.
Key Information
Challenges for analyzing causal heterogeneity
- It is nontrivial and challenging to identify important subgroups from a large number of subgroup candidates.
- the identification model can hardly communicate with humans due to the lack of interpretability
Existing work is insufficient to address these challenges. Automated heterogeneous treatment effect (HTE) estimation methods, such as causal trees [2] and causal forests [57], mainly construct hierarchical structures for individuals in datasets and identify leaf nodes in the hierarchies as subgroups. However, not all leaf nodes can reflect a significant treatment effect, leading to less useful results. Therefore, users still need to go through tedious review and analysis to find subgroups that meet their requirements. Subgroup discovery methods [6, 22, 55] can directly optimize correlation objectives but lack attention to the more complex causal effects that require statistical inference and confounding bias correction. Some researchers use visualization to assist causal analysis, but they either focus on the representation of causal graph structure [58, 66, 59, 37], manual selection of variables to divide subgroups [29], or clustering to obtain subgroups whose meaning is difficult to describe [28]. Therefore, how to support the cooperation between human intelligence and computing power in the analysis of HTE is still underexplored.
In this work, we propose a visual analytics approach for subgroup-based causal heterogeneity exploration that supports users in effectively identifying optimal subgroups from observational data, comparing and ranking different subgroups, and verifying treatment effects. First, we propose a causal subgroup discovery model based on constrained multi-objective optimization (MOO). Subgroups are described by interpretable rules, where the rule antecedents are conjunctions containing covariates and corresponding values, and the consequents correspond to subgroup evaluation metrics, such as effects and variances. Coverage and antecedent length are used as constraints to ensure interpretability. Due to multiple objectives and constraints, the optimal Pareto front of the subgroup is learned by a heuristic searching algorithm for user analysis. Second, we design and develop an interactive prototype system, Causal Prism, which incorporates intuitive visualizations of subgroups, evaluation metrics, and explanations of treatment effects, thereby facilitating users’ understanding, comparison, and verification of causal subgroups. Quantitative experiments, case studies, and expert interviews demonstrate the effectiveness and usability of the proposed model and system. In summary, our contributions are as follows:
- We propose a subgroup discovery model based on constrained multi-objective optimization, which can mine rule-explained subgroups with significant treatment effects from a large amount of high-dimensional observational data that outperforms state-ofthe-art methods.
- We designed and implemented an interactive visual analytics prototype system, CausalPrism, which includes table-based subgroup visualization, multi-attribute ranking, and matching unitbased explanation of treatment effects. The system supports users in understanding, comparing, and validating causal subgroups. Its utility has been proved through case studies, and positive feedback has been received during expert interviews.
Key Information
Key Work of this paper
propose a visual analytics approach for subgroup-based causal heterogeneity exploration
characters:
- supports users in effectively identifying optimal subgroups from observational data,
- comparing and ranking different subgroups,
- verifying treatment effects.
Components of the work:
- we propose a causal subgroup discovery model based on constrained multi-objective optimization (MOO).
- we design and develop an interactive prototype system, Causal Prism, which incorporates intuitive visualizations of subgroups, evaluation metrics, and explanations of treatment effects, thereby facilitating users’ understanding, comparison, and verification of causal subgroups.
Related Work
2.1 Heterogeneous Treatment Effect Estimation
Treatment effects vary across the whole population. Conditional average treatment effect (CATE), individual average treatment effect (ITE) and causal rules comprise current HTE research. Reviews [30,68] offer in-depth analyses of causal inference.
CATE evaluates treatment effects on specific subgroups of the population, given similar covariates like demographics. To optimize the heterogeneity of treatment effects, tree-based methods [2, 3, 57] are commonly employed to partition the covariate space into subspaces. For instance, Causal Tree [2] constructs the tree and estimates treatment effects in each subspace using separate data, avoiding overfitting by cross-validation. Wager et al. [57] suggested Causal Forest, combining causal tree ensemble results for more robust and smooth estimation. Root-to-leaf node routes naturally define subgroups of heterogeneous CATEs, making the tree model interpretable. However, tree-based methods may have limited performance due to greedy tree building process and does not necessarily return the “optimal” structure.
ITE compares outcomes with and without treatment. Since only one outcome is visible, another must be estimated. Existing techniques are single- or multi-model-based depending on whether treatment and control groups are estimated independently. The former uses regression to fit treatment effects. For example, Hill et al. [33] employs Bayesian additive regression trees to fit the outcome surface. The latter fits the treated and control groups separately, achieving better performance for significant differences between groups’ outcomes. The base model uses off-the-shelf estimators like linear regression [12] or neural networks [38]. With well-tuned parameters, these models can accurately estimate effects but are uninterpretable.
Several researchers have tried to find causal rules in data. For example, CRE [9] is a two-stage method that first produces rules using methods such as random forest or Gradient Boosting Machines, then picks robust ones using stability selection regularization. After mining association rules from data, Li et al. [46] conducted a cohort study to test whether the association rules were causal.
Many methods have presented estimators that can accurately estimate HTE despite confounding biases. We leverage existing estimators but focus on finding subgroups with significant treatment effects among many candidates. We present a constrained MOO-based causal subgroup discovery model that outperforms tree-based and black-box approaches in significance and interpretability.
2.2 Visual Causality Analysis
Automated causal detection algorithms are built upon assumptions and complex causal mechanisms that are hardly fulfilled in real life, causing accuracy and interpretability issues. Visualizations have been used to explore and verify causality interactively, which can be divided into homogeneous and heterogeneous causality investigations.
Homogeneous causality assumes that data’s causal mechanism is static and stable. Visualization helps users grasp complex causal relationships and make decisions. Graph-based visualizations [7,35,58,66] have been widely used to demonstrate causality in multi-attribute datasets, emphasizing the use of statistics to locate and manipulate improper relationships for what-if analysis. They employ advanced layout designs to highlight attribute distributions and enhance graph readability. In addition, design factors like node size [39], edge shape [8], and crowd beliefs [70] affect users’ understanding of causal relationships. Bar charts and scatter plots are also used to infer causality [40, 67, 69]. However, these approaches lack generalizability due to population variances such as demographics and environmental factors.
Heterogeneous causality examines causal relationships or effects that vary over time or data subgroups. Most work examines causal structural heterogeneity. In Causal Structure Investigator [59], users can acquire data subdivisions through manual filtering and k-means clustering. Then, these subdivisions are mapped to causal graphs for detailed analysis of causal paths. Jin et al. [37] focus on subsets in event sequences. Overlapping adjacency matrices with inner and outer sections lets users easily identify the differences in causal relationships between subsets. Deng et al. [19] created causal graph bands with compass glyphs for spatio-temporal sequences to show dynamic causal relationships in period-based time windows. This helps users understand influence transmission and identify spurious causalities. DOMINO [60] applies time delays and event constraints to temporal causality analysis, facilitating hypotheses formulation and validation.
Other research examines causal inference heterogeneity. The Absolute Standardized Mean Difference (ASMD) plot is used to assess covariate balance in groups after weighting and propensity score matching [25,52]. Guo et al. [28] created VAINE to enable users to find statistical phenomena like Simpson’s paradox by manually selecting clusters in covariate projections and observing their impact. Causalvis [29], a later proposal, enables the visualization of a whole causal analysis workflow. The raincloud and beeswarm plots in the Treatment Effect Explorer module let users manually pick subgroups faceted by covariates and analyze ITE distribution to examine heterogeneity.
However, the present HTE visualization work involves timeconsuming manual participation to locate subgroups, and the subgroups obtained through clustering lack explicit interpretable descriptions. Therefore, we propose CausalPrism to automatically obtain rule-described subgroups with significant treatment effects through optimization and design visualizations for subgroup exploration, comparison, and treatment effect validation.
2.3 Subgroup Discovery and Visualization
Subgroup discovery (SD) is a descriptive data mining method that finds data subgroups with intriguing patterns on certain goals, as summarized in comprehensive surveys [4, 32]. Data subgroups can be represented using description languages like attribute-value pairs and logical forms(e.g., conjunctions, inequalities, and fuzzy logic). Subgroup interestingness can be measured using binary, nominal, or numerical targets. Post-processing methods have been applied to select diverse and less redundant subgroups. Search methodologies like exhaustive and heuristic search have been used due to the large number of candidate subgroups.
Using the exhaustive techniques [6,26,27,62], all possible subgroups are searched. Since viable subgroups are exponentially large, a naive exhaustive search is time-consuming. Minimum support, optimistic estimate pruning, and generalization-aware pruning can reduce the hypothesis space. SD-Map [6] is an exhaustive SD approach that uses depth-first search to produce candidates, extending the Frequent Pattern (FP) Growth-based association rule mining method. The SD-Map* [5] is extended with binary, categorical, and continuous target variables.
Further studies [18, 22, 43, 55, 72] employed efficient heuristic methods. For example, DSSD [55] uses beam search, which starts with an initial solution and subsequently spreads to several candidates. Top performers are kept for the next iteration until a stopping condition is reached. SDIGA [18] is an evolutionary fuzzy rule induction method that facilitates the discovery of general rules by allowing variables to take multiple values. Subgroups can be evaluated in terms of confidence, support, and unusualness. Visualization techniques have also been proposed in order to support subgroup-level analysis tasks, such as subgroup multi-feature visualization [21, 24], model diagnosis on data subsets [14, 20, 42, 54, 71], and high-dimensional data subspace exploration [47, 64, 65]. For example, Taggle [21] employs a tabular visualization design that allows for hierarchical grouping and sorting of massive amounts of data. The icicle plot [20] and the map-based metaphor [47] provide help for comparisons between subgroups.
However, most SD methods only focuse on correlations, involving just covariates and outcomes. It is unsuitable for SD in causal scenarios (treatment, covariates, and outcomes must be considered). To this end, we formulate causal SD as a constrained MOO problem that can be efficiently solved using heuristic search. A range of subgroup visualization techniques, such as multi-attribute ranking [24], are incorporated into the CausalPrism system to help users explore and compare subgroups.
3 BACKGROUND
3.1 Preliminaries
We introduce the basis of causal inference under the potential outcome (PO) framework [51] and give examples based on medical scenarios.
A unit is an individual or object under study. A medical study unit may be a patient. The subscript 𝑖 denotes the 𝑖-th unit.
A treatment is an intervention or exposure that subjects to a unit. A new medicine or therapy could be used as a treatment in a medical study. Let a binary 𝑇 indicate whether a unit has received a treatment. Units satisfying 𝑇 = 1 belong to the treatment group, while those 𝑇 = 0 belong to the control group.
Outcomes are what would happen to units under different treatments. Each unit has two potential outcomes: factual outcome and counterfactual outcome. For instance, patient survival time is an outcome in a medical study. The potential outcome with treatment is 𝑌 (𝑇 = 1), also abbreviated as 𝑌 (1), and without treatment, it is 𝑌 (0).
Covariates are background variables that affect treatment assignment and outcome. For example, patient demographic information such as age may influence medication use (treatment assignment) and blood pressure (outcome). Observational studies often control for covariates to mitigate confounding and provide more unbiased effects estimates. Covariates are represented as a vector X𝑖 = (𝑥𝑖,1, · · · , 𝑥𝑖,𝑑), where 𝑑 is the number of covariates.
Observational data refers to data collected without the researcher manipulating the environment or the subjects being studied. It differs from RCTs, which randomly assign treatment to each unit. The observational data containing 𝑛 units is denoted by D = {(𝑇𝑖 ,X𝑖 ,𝑌𝑖)}𝑛 𝑖=1 .
Treatment effect refers to the impact of a treatment on an outcome. It can be obtained by quantitatively comparing the potential outcomes in the treatment and control conditions at different levels, such as populations, subgroups, and units. For unit 𝑖, its individual treatment effect (ITE) is defined as: 𝜏𝑖 = 𝑌𝑖(1) −𝑌𝑖(0). (1)
Unfortunately, for any unit, only one of the two potential outcomes can be observed, so ITE is not identifiable. One way to address this lack of counterfactual outcomes is to estimate the average treatment effect (ATE) on the population, defined as follows:
𝜏 = E[𝑌 (1) −𝑌 (0)]. (2)
ATE may fail to accurately reflect treatment effects due to the heterogeneity of units. This is overcome by conditional average treatment effect (CATE) on subgroups, which is defined as follows: 𝜏(x) = E[𝑌 (1) −𝑌 (0) | X = x]. (3)
Propensity score is a balancing score 𝑒(x) = 𝑃(𝑇 = 1 | X = x), defined as the conditional probability of getting a treatment given the covariates. In observational data, a biased treatment effect would be obtained by directly using the difference between the average outcome of the treatment and control groups because the treatment assignment is correlated with covariates. Rubin et al. [10] proved that {𝑌 (0),𝑌 (1)} ⊥ 𝑇 | 𝑒(X) under the assumption of unconfoundedness. For binary treatment, the Logistic regression model is commonly used to estimate propensity scores [13].
Outcome Variance refers to the outcome variability among the units in the treatment and control group. A lower variance means that the treatment leads to a more consistent outcome among units. Let 𝜎 2 be the variance.
Causal Subgroup refers to specific subgroups within the population that exhibit significant treatment effects. For example, the preventive effect of influenza vaccine is more significant in the elderly and immunocompromised people. S is used to represent subgroups.
3.2 Design Requirements
We distilled the design requirements from interviews with three experts (E1-3) and a literature review. Data analysts E1 and E2 have three years of work experience in a technology firm. Their daily tasks include evaluating KPI anomalies and guiding advertising placement using causal analysis on observational data. E3, a university associate professor, has written multiple causal inference studies. They noted that causal inference is plagued by data heterogeneity, and massive amounts of observational data lack appropriate exploration tools. Causality interpretability is also crucial since users cannot make decisions if they don’t trust the result. Finally, the requirements are listed.
R1 Descriptive subgroup identification. Observational data usually contains a large potential exploration space with many variables. Although traditional data clustering methods can be used to discover clusters, they do not give a corresponding interpretation. Experts mentioned that “Although high-value groups can be manually segmented based on domain knowledge, it often requires multiple attempts of different filtering conditions.” Users can take advantage of automatically identified subgroups to further discover interesting causal patterns.
R2 Subgroup understanding and valuation. Subgroups involve rich information such as variables used in subgroup descriptions, value distribution of covariates, treatment effect, and variance scores. Users should be able to browse such information to understand the characteristics of a subgroup. It is necessary for the system to provide a clear and intuitive visualization for subgroups.
R3 Subgroup adjustment and hypothesis. The subgroups automatically discovered by the model may not satisfy users. Experts say that for advertising scenarios, they aim to boost user spending and meet total profit goals. Therefore, when necessary, they will relax the filtering conditions or merge small groups to enlarge the target subgroup. Our approach needs to support users to adjust subgroups. The basis of adjustment could be the understanding of the target subgroup, domain knowledge from users, or the analysis results of what-if tests on new subgroups.
R4 Subgroup comparison and ranking. Users have diverse preferences for causal subgroups. For example, when determining the target audience for advertising, conservative users are willing to choose subgroups that are generally effective and have smaller variances, while risk-takers try subgroups that have stronger effects but may also have greater outcome fluctuations. Therefore, we need to allow users to compare subgroups from multiple perspectives and rank them based on their preferences to select satisfactory subgroups.
R5 Treatment effect validation. Users need to understand why certain treatment effect is estimated and be provided with data evidence to explain their rationality. In addition, the estimated treatment effect may be biased by the size and distribution of the data units. Seeking reliable conclusions, visualizations are needed to help users rule out suspicious causal effects.
