Project

HaiyueAugust 25, 2023About 9 min

Dataset

BRCA-50 is a Breast cancer dataset, including the expression levels of 50 important genes in Breast cancer.

The dataset includes 1212 samples with
112 samples are of normal cases (class = N) and
1100 samples are of cancer patients (class = C).

Tasks

Load library

library(tidyverse)
library(gRain)
library(pcalg)
library(bnlearn)

Load data

data <- read_csv("https://seamice.github.io/data/unisa/AdvancedAnalytic2/project/BRCA_RNASeqv2_top50.csv", col_names = TRUE)
data_no_class <- data %>% select(-class)

Task 1: Causal Structure (CPDAG)

Use a causal structure learning algorithm to find the gene regulatory network, i.e. the network showing the interactions between genes, using the gene expression data. Explain how the algorithm works. (4)

Hints

Hints: Please exclude the class variable in building the network

1.1 Learn the structure

Select the PC algorithm to learn the CPTAG

pc.fit <- pc(
  suffStat = list(C = cor(data.no.class), n = nrow(data.no.class)), 
  indepTest = gaussCItest, 
  alpha=0.01, 
  labels = colnames(data.no.class)
  #labels = as.character(1:50)  #label node names
)

#data.frame(NUM=1:50, NAME=colnames(data.no.class))
plot(pc.fit, main = "CPDAG")

1.2 Explain how the algorithm works

PC algorithm is an approach to learn the graph from a data set. The algorithm could be plit into two parts. The first part is to learn the correlation among variables, which is lso called learning skeleton. The second part is to find the direction of the elationship, which is also called as orientating the edges.

For this case,

Learning skeleton

Input: Data set D, significant level alpha
Output: The undirected graph G with a set of edges E

The first part, the alpha has been set alpha = 0.01, depth = 0, D is the data consist of all variables. Assume that all variables are correlated, the correlation set is E*.

Repeat
- for each edges in Graph G, test the
  - If number of nodes in E is greater or equal depth + 2 jump to NextLevel, else continue.
    - Test the independence of all nodes pairs from E given condition depth count combination of other variables from E.
    - If the independence exist,
      1. remove the correlation from the E.
      2. Save the condition as the seperation of the two nodes of the edge.
    - End If
  - End IF
- NextLevel : set depth = depth + 1
Until, If number of Node in E is less then depth + 2 stop, else continue Repeat.

Finally, get the skeleton of the graph G.

Orientating the edges

Input: Skeleton G, seperation sets S
Output: CPDAG G*

for all nonadjacent variables X, Y with a common neighbor K do
- If K does not belongs to separation set of the two nodes S(X,Y) then
  Replace X-K-J in G by X->K<-Y
- end
end

Next, orient as many other undirected edges as possible using the following rules:

Orient X-Y into X->Y if exists Z->X, Z and K are onadjacent.
Orient X-Y into X->Y, if exists a chain X->Z->Y.
Orient X-Y into X->Y, if exists two chains X-Z->Y and X-A->Y, nd Z and A are nonadjacent.

Finally, get a CPDAG G*

Task 2: Causal Effects (IDA)

EBF1 is an important gene that is involved in many biological processes leading to cancer. Find the top 10 other genes that have strong causal effects on EBF1 using a causal inference algorithm. (4)
Hints
- Exclude the class variable in building the network
- If there are multiple possible causal effects between the cause and the effect, we can use the minimum of the absolute values (of the causal effects) as the final result
- The causal effects are normally ranked based on their absolute values.
Solution: Using ida to calculate the causal effects of all other variables on EBF1 based on the graph built from task 1, then sort the final result base on the values come from ida algorithm.
```
# Get gene EBF1 index
EBF1_idx <- match("EBF1", names(data.no.class))
CausalOnEBF1 <- data.frame(
  causality = unlist(
    lapply(
      (1:50)[-EBF1_idx], 
      function(idx){
        min(
          abs(
            idaFast(
              idx,
              EBF1_idx,
              cov(data.no.class),
              pc.fit@graph)
          )
        )
      }
    )
  ),
  variable  = names(data.no.class)[-EBF1_idx]
) 
CausalOnEBF1 %>% 
  arrange(across(causality, desc))

(CausalOnEBF1 %>% 
  arrange(across(causality, desc)))$variable[1:10]
```
According to the result, it could easily get the top 10 genes have strongest causal effects on EBF1 are FXYD1, ABCA10, TMEM220, ARHGAP20, FIGF, KLHL29, GPIHBP1, TMEM132C, RDH5, ABCA9.

Task 3: Local Causal Structure & Markov blanket

Use a local causal structure learning algorithm to find genes in the Markov blanket of ABCA9 from data. Explain how the algorithm works. (4)

Solution: We could use local structure learning algorithm IAMB to get the Markov blanket of ABCA9 from the data

3.1 Calculating the Markov Blanket

data.num <- data %>% select(-class)
data.num$class <- ifelse(data$class == 'C', 1, 0)
ABCA9.mb <- learn.mb(
    data.frame(data.num),
    "ABCA9",
    method = "iamb", 
    alpha = 0.01
)
ABCA9.mb

According to the result above, the Markov Blanket of ABCA9 has 23 nodes.

3.2 Explanation

The IAMB is an abbreviation for Incremental Association Markov Blanket, the algorithm could be separated into two phases, the Growing pahse and Shrinking phase. Details for the two phases are below:
CMI: Conditional mutual information

Input: dataset D; target T
Output: MB(T)

Growing Phase:

Repeat till MB(T) does not change
- Find the node X from dataset D [exclude all the nodes in MB(T) and T]{style="color:red"} that has the maximum CMI
- IF X independence with T given MB(T), Then
  - Add X to MB(T)
- End IF

Shrinking Phase:

For each node X from MB(T)
- IF X independence with T given MB(T) [exclude]{style="color:red"} X, Then
  - Remove X from MB(T)
- End IF
End For

Finally, get the final MB(T).

References

[01]. An Improved IAMB Algorithm for Markov Blanket Discovery

[02]. Discovering Markov Blankets: Finding Independencies Among Variables

Task 4: Discrete the dataset

Discretise the dataset to binary using the average expression of ALL genes as the threshold. The discretised dataset will be used in the following questions.

Solution:
Step 1: Calculating the mean
Step 2: Discrete the data (1: $\gt$ mean 0: $\lt$ mean)

Because of the pcSelect method only support numeric variables, so the discrete variables need to be replaced with 1 and 0 according to step 2.

# The mean of each gene
# mean.val <- as.data.frame(apply(data.no.class, 2, mean))
# The mean of All genes
mean.val <- mean(apply(data.no.class, 2, mean))
names <- colnames(data.no.class)

data.binary <- as.data.frame(
  sapply(
    colnames(data.no.class), 
    function(x) ifelse(data.no.class[,x] >mean.val, 1, 0)
))
data.binary$class <- ifelse(data$class == 'C', 1, 0)


#data.binary.c <- as.data.frame(
#  sapply(
#    colnames(data.no.class), 
#    function(x) ifelse(data.no.class[,x] >mean.val, 'T', 'F')
#))
#data.binary.c$class <- ifelse(data$class == 'C', 'T', 'F')

Task 5: PC-Simple

Use PC-simple algorithm (pcSelect) to find the parent and children set of the class variable. Explain how PC-simple works.
- Evaluate the accuracy of the Naïve Bayes classification on the dataset in the following cases:
  1. Use all features (genes) in the dataset
  2. Use only the features (genes) in the parent and children set of the class variable
- Compare the accuracy of the models in the two cases using 10-fold cross validation. (6)

References:

5.1 Find the parents and children

class.pc <- pcSelect(
  data.binary %>% select(class),
  data.binary %>% select(-class),
  alpha = 0.01
)
class.pc <- data.frame(ispc = class.pc$G, zmin = class.pc$zMin)
class.pc[order(class.pc$zmin, decreasing=TRUE),]

rownames(class.pc[class.pc$ispc == TRUE,])

According to the result above, it could easily found that the parents and children of class variable are FIGF, ARHGAP20, CD300LG, KLHL29, CXCL2, ATP1A2, MAMDC2, TMEM220, SCARA5, ATOH8.

5.2 Explanation of PC-Simple

PC-Simple is an algorithm to find the parents and children of a target node via conditional independence tests base on a threshold alpha,

Input: Dataset D consist of set of predictor variables X and target variable Z; a significant levle alpha for conditional independence test.
Output: The parents and children set PC of target Z

For this case, the alpha has been set 0.01, k = 0 , PC(k) equals all other variables.

Repeat if count of PC is greater than k
- k = k+1
- PC(k) = PC(k-1)
- For each node X from PC(k-1)
  - For each combination nodes S from PC(k-1) excludes X and count of S equals k-1
    - IF X and Z are independent given S at significance level alpha, Then
      - remove X from PC(K)
    - End IF
  - End For
- End For

The PC is the final result.

5.3 Naïve Bayes classification

library(caret)

5.3.1 Naive Bayes classification with all features

set.seed(100)
trctrl <- trainControl(method = "cv", number = 10, savePredictions=TRUE)
nb_all <- train(
  factor(class) ~., 
  data = data.binary, 
  method = "naive_bayes", 
  trControl=trctrl, 
  tuneLength = 0
)
nb_all

data.binary.related <- data.binary[,append(rownames(class.pc[class.pc$ispc == TRUE,]), "class")]
nb_pc <- train(
  factor(class) ~., 
  data = data.binary.related, 
  method = "naive_bayes", 
  trControl=trctrl, 
  tuneLength = 0
)
nb_pc

5.3.3 Comparision between the two models

confusionMatrix(nb_all)
confusionMatrix(nb_pc)

According to the confusion matrix, we could get indicators table like below.

indicators	ma	mr
accuracy	0.9761	0.9843
precision(1) : cancer	0.9982	0.9809
precision(0): normal	0.7589	1
recall(1): cancer	0.9760	1
recall(0): normal	0.9770	0.8421

The precision stands for the accuracy of prediction cases, the recall represents the accuracy of actual cases that has been recognized. According to the table above, the overall accuracy of mr is better than ma. For cancer cases, the ma perform better than mr on prediction, but for recall value of mr is better than ma. For normal cases, the mr works better than ma on precision, but the ma perform better on recall than mr.

Task 6: Calculating based on specified DAG

Given a Bayesian network as in the below figure

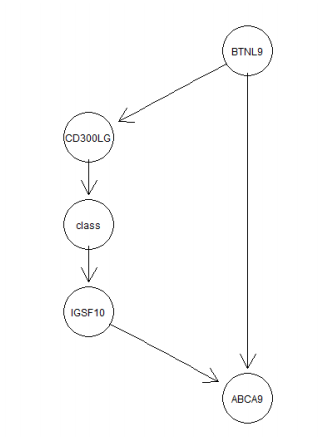
6.1 a) Construct the conditional probability tables for the Bayesian network based on data. (3)

6.1.1 Construct using `gRain`

For constructing the net, using the T instead of 1 and using F instead of 0.

data.graph <- data.binary %>% select(BTNL9,CD300LG,class,IGSF10,ABCA9)

yn <- c('T','F')

B     <- cptable(~BTNL9, 
                 values= (data.graph %>% 
                            select(BTNL9) %>%
                            group_by(BTNL9) %>%
                            count() %>%
                            arrange(across(BTNL9, desc)))$n,
                 levels=yn)
CD.B  <- cptable(~CD300LG|BTNL9, 
                 values=(data.graph %>% 
                            select(CD300LG, BTNL9) %>%
                            group_by(CD300LG, BTNL9) %>%
                            count() %>%
                            arrange(across(BTNL9, desc),
                                    across(CD300LG, desc)))$n,
                 levels=yn)
c.CD  <- cptable(~class|CD300LG, 
                 values=(data.graph %>% 
                            select(class, CD300LG) %>%
                            group_by(class, CD300LG) %>%
                            count() %>%
                            arrange(across(CD300LG, desc),
                                    across(class, desc)))$n, 
                 levels=yn)
I.c   <- cptable(~IGSF10|class, 
                 values=(data.graph %>% 
                            select(IGSF10, class) %>%
                            group_by(IGSF10, class) %>%
                            count() %>%
                            arrange(across(class, desc), 
                                    across(IGSF10, desc)
                                    ))$n, 
                 levels=yn)

AB.B_I<- cptable(~ABCA9|BTNL9:IGSF10,
                 values=(data.graph %>% 
                            select(ABCA9, BTNL9,IGSF10) %>%
                            group_by(ABCA9, BTNL9,IGSF10) %>%
                            count() %>%
                            arrange( 
                              across(IGSF10, desc), 
                              across(BTNL9, desc),
                              across(ABCA9, desc)))$n,
                 levels=yn)

plist <- compileCPT(list(B, CD.B, c.CD, I.c, AB.B_I))
plist
net=grain(plist) 

plot(net$dag)

6.1.2 Construct using `bnlearn`

bn.dag = model2network("[BTNL9][CD300LG|BTNL9][ABCA9|BTNL9:IGSF10][class|CD300LG][IGSF10|class]")
graphviz.plot(bn.dag)

learn parameters from data

bn.fitted <- bn.fit(
  bn.dag,
  data.binary %>% select(BTNL9, CD300LG, class, IGSF10, ABCA9)
)

6.2 b) Estimate the probability of the four genes in the network having high expression levels. (2)

This question aims to calculate the joint probability of the four genes in the network for each value of the four variables equal T. It could be expressed with the formula P(BTNL9=T, CD300LG=T, IGSF10=T, ABCA9=T).

6.2.1 Method 1

querygrain(net, nodes=c("BTNL9", "CD300LG", "IGSF10", "ABCA9"), type="joint")

According to the table above, it could get the P(BTNL9=T, CD300LG=T, IGSF10=T, ABCA9=T)=0.073736

6.2.2 Method 2

joint_pb <- setEvidence(
  net, 
  evidence=list(BTNL9="T", CD300LG="T",  IGSF10="T", ABCA9="T")
)
pEvidence(joint_pb)

According to the table above, it could get the same result with method 1.

6.3 c) Estimate the probability of having cancer when the expression level of `CD300LG` is high and the expression level of `BTNL9` is low. (2)

This question actually ask us to calculate the conditional probability P(class=T| CD300LG=T, BTNL9=F), here I will use cpquery method for get the conditional probability.

querygrain(net, nodes=c("class","CD300LG","BTNL9"), type="conditional")

So the final result P(class=T|CD300LG=T,BTNL9=F) = 0.2585034

6.4 d) Prove the result in c) mathematically. (2)

data.graph %>% 
  select(class, CD300LG,BTNL9) %>%
  group_by(class, CD300LG,BTNL9) %>%
  count() %>%
  arrange( 
    across(class, desc), 
    across(CD300LG, desc),
    across(BTNL9, desc))
#plot(net$dag)

According to the graph, BTNL9 is the parent of CD300LG, so

P(class=T| BTNL9=F,CD300LG=T)
= P(class=T|CD300LG=T)
= (32+6)/(32+107+6+2)
= 0.2585034

6.5 e) Given we know the value of `CD300LG`, is the “class” conditionally independent of `ABCA9`? And why? (3)

Anwser: No

Explanation: According to Markov condition, every node in a Bayesian network is conditionally independent of its nondescendants, given its parents. So the parent CD300LG of class is given, ABCA9 is the descendant of class variable, so the class is not conditionally independent of ABCA9.

Download RMD
online code

References

Algorithm:
http://www.sci-princess.info/wp-content/uploads/Causal-Graphs-and-the-PC-Algorithm.pdf
https://pooyanjamshidi.github.io/csce580/lectures/CSCE580-GuestLecture--BNLearning.pdf
https://arxiv.org/pdf/0908.3817.pdf
https://www.bnlearn.com/about/slides/slides-useRconf13.pdf

pcalg:
https://stat.ethz.ch/Manuscripts/buhlmann/pcalg-software.pdf
https://cran.r-project.org/web/packages/pcalg/pcalg.pdf
https://cran.r-project.org/web/packages/pcalg/vignettes/vignette2018.pdf

bnlearn:
https://www.bnlearn.com/examples/graphviz-plot/
https://www.bnlearn.com/documentation/man/cpquery.html
https://rdrr.io/github/vspinu/bnlearn/man/cpquery.html
https://dipartimenti.unicatt.it/scienze-statistiche-23-25-1-17ScutariSlides.pdf

Graphviz
https://rdrr.io/bioc/Rgraphviz/man/GraphvizAttributes.html#:~:text=Font size%2C in points%2C for,Label for the graph.
https://www.cs.cmu.edu/afs/cs/project/jair/pub/volume18/acid03a-html/node2.html

Chinese Sample:
https://www.cnblogs.com/payton/articles/4608383.html

Project

Requirements

Instructions

Marking Guide

Dataset

Tasks

Load library

Load data

Task 1: Causal Structure (CPDAG)

1.1 Learn the structure

1.2 Explain how the algorithm works

Task 2: Causal Effects (IDA)

Task 3: Local Causal Structure & Markov blanket

3.1 Calculating the Markov Blanket

3.2 Explanation

References

Task 4: Discrete the dataset

Task 5: PC-Simple

5.1 Find the parents and children

5.2 Explanation of PC-Simple

5.3 Naïve Bayes classification

5.3.1 Naive Bayes classification with all features

5.3.3 Comparision between the two models

Task 6: Calculating based on specified DAG

6.1 a) Construct the conditional probability tables for the Bayesian network based on data. (3)

6.1.1 Construct using `gRain`

6.1.2 Construct using `bnlearn`

6.2 b) Estimate the probability of the four genes in the network having high expression levels. (2)

6.2.1 Method 1

6.2.2 Method 2

6.3 c) Estimate the probability of having cancer when the expression level of `CD300LG` is high and the expression level of `BTNL9` is low. (2)

6.4 d) Prove the result in c) mathematically. (2)

6.5 e) Given we know the value of `CD300LG`, is the “class” conditionally independent of `ABCA9`? And why? (3)

References